What are AR Coatings and how are they used with Synthetic Sapphire in various applications?
If you want to learn more, you’re in the right place.
Overview
This paper provides an overview of AR coating and how it can be used with synthetic sapphire. Additionally, we will review the properties, benefits and types of AR coating along with various applications for its use.
Understanding synthetic sapphire and AR coating
Synthetic sapphire is useful in many applications requiring hardness and chemical inertness. Coupling the mechanical advantages of sapphire
with the material’s optical properties as a window material supports applications that require protection of visual arrays, e.g., mobile phone
screens, wrist watches, or isolation of environments where optical techniques are used to measure or modify within the isolated environment, e.g., flow
cells. Depending on the application, high optical efficiencies and/or reduction of stray light may require anti-reflective (AR) coatings to enhance sapphire window performance. We will discuss the physics of AR coatings and how they improve transmission efficiency and reduce stray light.
The first documented observation of AR coating behavior was recorded by John William Strutt Rayleigh in 1886 when he noted the transmission efficiency of glass was higher when surface tarnish was present on the glass surface. Understanding the phenomenon provided a foundation for later inventions and improvements in producing AR coatings at scale.

In 1886, Lord Rayleigh discovered the advantages of thin films on glass to improve transmission efficiency.
So how can tarnished glass transmit light more efficiently? The cause of this is related to the wave nature of light and the reflective nature of certain materials. When light is incident upon a transparent material’s surface at smaller angles of incidence, a significant percentage of the light propagates through the material, changing angle as it enters and leaves the material based on refractive index (Snell’s Law). A smaller percentage is reflected off the surface at an angle equal to the angle of incidence. Depending on the surface finish of the material, additional light can be lost due to surface scatter (haze).

Visualize the windshield of a car. When looking through the glass where curves occur, there is distortion of the image being viewed.
This is related to Snell’s Law and how the angle of the image rays change based on the curved surface angles. When you are observing another car’s windshield, and the sun hits at an angle the reflects light to your eyes, you can be blinded by the reflection. Finally, imagine the window glass is dirty and covered with road oil and grime. The glass appears hazy, and it is difficult to see through it clearly when light scatters off the contaminants, scratches, and pits on the glass surface.
If we want to maximize the amount of light transmitted through a transparent material (sapphire window), while reducing the amount of reflected light, we apply a coating of deliberate thickness and refractive index. A “perfect” coating can be calculated, but in practice, available coating materials, coating adhesion, and current coating processes limit attainment of theoretical nominal. Additionally, we want to ensure the window is polished and free of contaminants. The coating interacts with light waves to create destructive interference on the rays that would reflect to the observer and creates constructive interference on the waves that continue through the window, thereby reducing the reflected light, while increasing the amount of light transmitted through the sapphire window.

The figure above shows the destructive interference of light waves when the AR coating index of refraction and coating thickness are selected properly.
The image below was taken from the paper Multilayer Reflectivity by John E. Davis, which describes the following. “This figure shows the possible paths of a photon within a multilayer that is composed of two dielectric slabs sandwiched between the vacuum at the top and a bulk substrate at the bottom. When the photon encounters the boundary between two layers, it either reflects or refracts. The shade and thickness of a photon line is used to denote the relative probability of the line.”

To determine how much light is reflected/transmitted, we can leverage equations derived from the work of Augustin-Jean Fresnel. Reflectance at a normal angle of incidence can be expressed as:
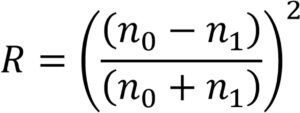
For this example, n0 is the refractive index of air (~ 1.00) and n1 is the refractive index of sapphire (~1.77). The reflectance at the interface between air and sapphire is ~7.7%. Calculating the exit of the light waves from the sapphire into air, we get another ~7.7%. For optically sensitive applications, reflectance of 8% is not trivial, and if needed, we would turn to the use of AR coatings to improve efficiency.
How then do we calculate the “perfect” AR coating? We will limit the depth of the discussion with a simple case and avoid digging too deep into the underlying physics, but a perfect, single layer coating can be calculated using the index of refraction of the transparent material to determine the nominal index of refraction for the coating, and the thickness of the AR coating will be ¼ the wavelength of the light waves we are seeking to optimize.
Assuming an index of refraction of 1.77 for a sapphire window, the coating refractive index would be √1.77=1.33. If we were using a green laser at wavelength of 532nm, then 532nm / 4= 133nm film thickness. Now we need a material with an index of refraction close to 1.33 and the ability to coat the sapphire surface with the material. Depending on the use of the window, we may want a coating that was durable, with a transparency over wide range of wavelengths. One material that meets these requirements in magnesium fluoride: an affordable option that can reduce reflectance of sapphire to 0.4%!
More complex AR coatings can be applied to sapphire by layering various materials to achieve optimized performance over various wavelengths, and in some cases, single layer coatings can be “tuned” over a range of refractive indices by controlling the microstructure of the coating.
Conclusion / Summary
Synthetic sapphire is a robust, versatile material that can deal with harsh conditions and is suitable for many applications such as sensors, cover lenses, viewports, pressure windows and subsea imaging systems. It can withstand very high temperatures and is very resistant to chemical acids/alkaloids, high pressure and strong vacuum environments. This hard material should be at the top of the list of design engineers looking for high performance in their specific applications at reasonable cost. AR coatings can further enhance the use of synthetic sapphire in a number of critical applications.
